欢迎来到南叶の小窝

1
int binarySearch(vector<int>& nums, int target) {
2
    // 一左一右两个指针相向而行
3
    int left = 0, right = nums.size() - 1;
4
    while(left <= right) {
5
        int mid = (right + left) / 2;
6
        if(nums[mid] == target)
7
            return mid;
8
        else if (nums[mid] < target)
9
            left = mid + 1;
10
        else if (nums[mid] > target)
11
            right = mid - 1;
12
    }
13
    return -1;
14
}

1
输入：nums = [2,7,11,15], target = 9
2
输出：[0,1]
3
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

1
输入：nums = [3,2,4], target = 6
2
输出：[1,2]

1
class Solution {
2
public:
3
    vector<int> twoSum(vector<int>& nums, int target) {
4
        vector<pair<int, int>> vec;//这里为了保留原数组的索引
5
        for (int i = 0; i < nums.size(); ++i)
6
            vec.push_back({nums[i], i});
7

8
        sort(vec.begin(), vec.end());
9

10
        int left = 0, right = vec.size() - 1;
11
        while (left < right) {
12
            int sum = vec[left].first + vec[right].first;
13
            if (sum == target) {
14
                return {vec[left].second, vec[right].second};
15
            } else if (sum < target) {
16
                left++;
17
            } else {
18
                right--;
19
            }
20
        }
21

22
    }
23
};

1
输入：s1 = "ab" s2 = "eidbaooo"
2
输出：true
3
解释：s2 包含 s1 的排列之一 ("ba").

1
输入：s1= "ab" s2 = "eidboaoo"
2
输出：false

1
class Solution {
2
public:
3
    // 判断 s 中是否存在 t 的排列
4
    bool checkInclusion(string t, string s) {
5
        unordered_map<char, int> need, window;
6
        for (char c : t) need[c]++;
7

8
        int left = 0, right = 0;
9
        int valid = 0;
10
        while (right < s.size()) {
11
            char c = s[right];
12
            right++;
13
            // 进行窗口内数据的一系列更新
14
            if (need.count(c)) {
15
                window[c]++;
16
                if (window[c] == need[c])
17
                    valid++;
18
            }
19

20
            // 判断左侧窗口是否要收缩
21
            while (right - left >= t.size()) {
22
                // 在这里判断是否找到了合法的子串
23
                if (valid == need.size())
24
                    return true;
25
                char d = s[left];
26
                left++;
27
                // 进行窗口内数据的一系列更新
28
                if (need.count(d)) {
29
                    if (window[d] == need[d])
30
                        valid--;
31
                    window[d]--;
32
                }
33
            }
34
        }
35
        // 未找到符合条件的子串
36
        return false;
37
    }
38
};

1
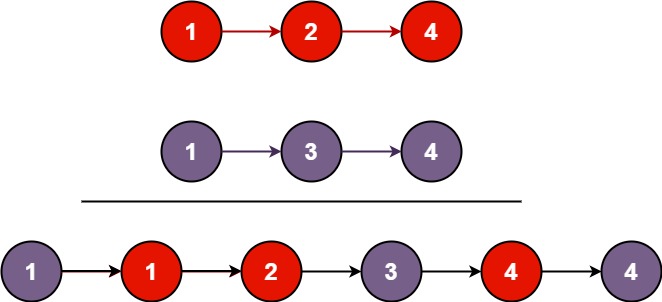
输入：l1 = [1,2,4], l2 = [1,3,4]
2
输出：[1,1,2,3,4,4]

1
输入：l1 = [], l2 = []
2
输出：[]

1
输入：l1 = [], l2 = [0]
2
输出：[0]

1
class Solution {
2
public:
3
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
4
        // 虚拟头结点
5
        ListNode dummy(-1), *p = &dummy;
6
        ListNode *p1 = l1, *p2 = l2;
7

8
        while (p1 != nullptr && p2 != nullptr) {
9
            // 比较 p1 和 p2 两个指针
10
            // 将值较小的的节点接到 p 指针
11
            if (p1->val > p2->val) {
12
                p->next = p2;
13
                p2 = p2->next;
14
            } else {
15
                p->next = p1;
16
                p1 = p1->next;
17
            }
18
            // p 指针不断前进
19
            p = p->next;
20
        }
21

22
        if (p1 != nullptr) {
23
            p->next = p1;
24
        }
25

26
        if (p2 != nullptr) {
27
            p->next = p2;
28
        }
29

30
        return dummy.next;
31
    }
32
};

1
输入：lists = [[1,4,5],[1,3,4],[2,6]]
2
输出：[1,1,2,3,4,4,5,6]
3
解释：链表数组如下：
4
[
5
  1->4->5,
6
  1->3->4,
7
  2->6
8
]
9
将它们合并到一个有序链表中得到。
10
1->1->2->3->4->4->5->6

1
输入：lists = []
2
输出：[]

1
class Solution {
2
public:
3
    ListNode* mergeKLists(vector<ListNode*>& lists) {
4
        if (lists.empty()) return nullptr;
5
        // 虚拟头结点
6
        ListNode* dummy = new ListNode(-1);
7
        ListNode* p = dummy;
8
        // 优先级队列，最小堆
9
        auto cmp = [](ListNode* a, ListNode* b) { return a->val > b->val; };
10
        priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq(cmp);
11
        // 将 k 个链表的头结点加入最小堆
12
        for (ListNode* head : lists) {
13
            if (head != nullptr) {
14
                pq.push(head);
15
            }
16
        }
17

18
        while (!pq.empty()) {
19
            // 获取最小节点，接到结果链表中
20
            ListNode* node = pq.top();
21
            pq.pop();
22
            p->next = node;
23
            if (node->next != nullptr) {
24
                pq.push(node->next);
25
            }
26
            // p 指针不断前进
27
            p = p->next;
28
        }
29
        return dummy->next;
30
    }
31
};

1
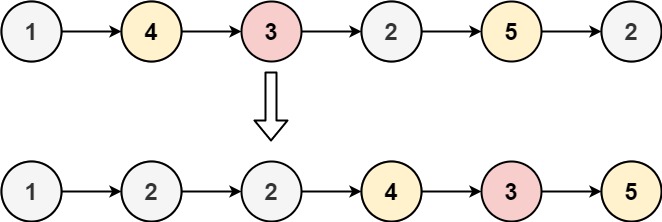
输入：head = [1,4,3,2,5,2], x = 3
2
输出：[1,2,2,4,3,5]

1
输入：head = [2,1], x = 2
2
输出：[1,2]

1
class Solution {
2
public:
3
    ListNode* partition(ListNode* head, int x) {
4
        // 存放小于 x 的链表的虚拟头结点
5
        ListNode* dummy1 = new ListNode(-1);
6
        // 存放大于等于 x 的链表的虚拟头结点
7
        ListNode* dummy2 = new ListNode(-1);
8
        // p1, p2 指针负责生成结果链表
9
        ListNode* p1 = dummy1, *p2 = dummy2;
10
        // p 负责遍历原链表，类似合并两个有序链表的逻辑
11
        // 这里是将一个链表分解成两个链表
12
        ListNode* p = head;
13
        while (p != nullptr) {
14
            if (p->val >= x) {
15
                p2->next = p;
16
                p2 = p2->next;
17
            } else {
18
                p1->next = p;
19
                p1 = p1->next;
20
            }
21
            // 不能直接让 p 指针前进，
22
            // p = p->next
23
            // 断开原链表中的每个节点的 next 指针
24
            ListNode* temp = p->next;
25
            p->next = nullptr;
26
            p = temp;
27
        }
28
        // 连接两个链表
29
        p1->next = dummy2->next;
30

31
        return dummy1->next;
32
    }
33
};